Shor’s Algorithm
Definition
Shor’s Algorithm is a quantum algorithm discovered by Peter Shor in 1994, designed to factor large integers and solve discrete logarithms in polynomial time on a quantum computer. This capability poses a significant threat to classical cryptography schemes, such as RSA and Diffie-Hellman, which rely on the infeasibility of factoring large numbers or computing discrete logarithms with classical computers.
Shor’s Algorithm exploits the power of quantum parallelism and the Quantum Fourier Transform (QFT) to find the period of a function related to the integer in question. By determining this period, it becomes possible to derive non-trivial factors of large numbers—or solve discrete logs—exponentially faster compared to any known classical algorithm.
Use Cases
Despite often being described in the context of breaking cryptography, Shor’s Algorithm has broader implications:
- Cryptanalysis: It is primarily famous for breaking RSA, Elliptic Curves Cryptography (ECC), and other discrete-log-based systems if (and when) large-scale quantum computers become practical.
- Post-Quantum Cryptography (PQC) Research: Shor’s Algorithm directly motivates the field of post-quantum or quantum-resistant cryptography, prompting the design of new cryptographic schemes believed to be secure against quantum attacks.
- Scientific and Academic: In quantum computing courses and research, Shor’s Algorithm is often used as a central illustration of how quantum algorithms can vastly outperform classical algorithms for certain problems.
Advantages
-
Exponential Speed-Up
- Classically, factoring an -bit integer grows super-polynomially. Shor’s Algorithm can factor an -bit integer in roughly steps (or better with optimizations), showcasing a significant theoretical advantage.
-
Demonstration of Quantum Superiority
- Alongside Grover’s Algorithm for unstructured search, Shor’s Algorithm remains a cornerstone example of how quantum computers can outperform classical systems for specific tasks.
-
Driving Innovation in Cryptography
- The cryptographic world now intensively researches lattice-based, code-based, or other post-quantum cryptosystems to stay ahead of the quantum threat.
Challenges
-
Quantum Hardware Requirements
- To factor large numbers (e.g., 2048-bit RSA moduli), you need thousands to millions of logical qubits with fault tolerance and low error rates—well beyond current quantum hardware capabilities.
-
Error Correction
- Real quantum systems suffer from noise and decoherence, necessitating robust quantum error correction schemes (e.g., the surface code). These in turn require many physical qubits to create a single logical qubit.
-
Implementation Complexity
- Designing, programming, and stabilizing a large-scale quantum circuit for Shor’s Algorithm is complex. Even with today’s quantum libraries, only small numbers (tens to hundreds of bits) can be factored reliably.
Applying Shor’s Algorithm to Cryptography
Challenges in Classical Cryptography
Modern cryptosystems like RSA, Diffie–Hellman Key Exchange, andElliptic Curves Cryptography rely on the hardness of factoring large integers or computing discrete logarithms. A classical computer cannot feasibly solve these problems for properly chosen key sizes (e.g., 2048-bit or higher). However, with Shor’s Algorithm:
- Factoring RSA Moduli: Breaking RSA requires factoring a large semi-prime . Shor’s Algorithm can do this in polynomial time, undermining RSA’s security assumptions.
- Discrete Log Problems: Similar logic applies to discrete log variants (e.g., Diffie–Hellman and ECC), making them vulnerable to quantum attacks.
How Shor’s Algorithm Works (High-Level)
- Choose a Random
- Select an integer coprime to (the integer to be factored).
- Quantum Period-Finding
- Construct and evaluate the function mod N$ within a quantum circuit.
- Use the Quantum Fourier Transform (QFT) to find the period of this function in superposition.
- Classical GCD
- Once the period is found, compute to discover non-trivial factors of .
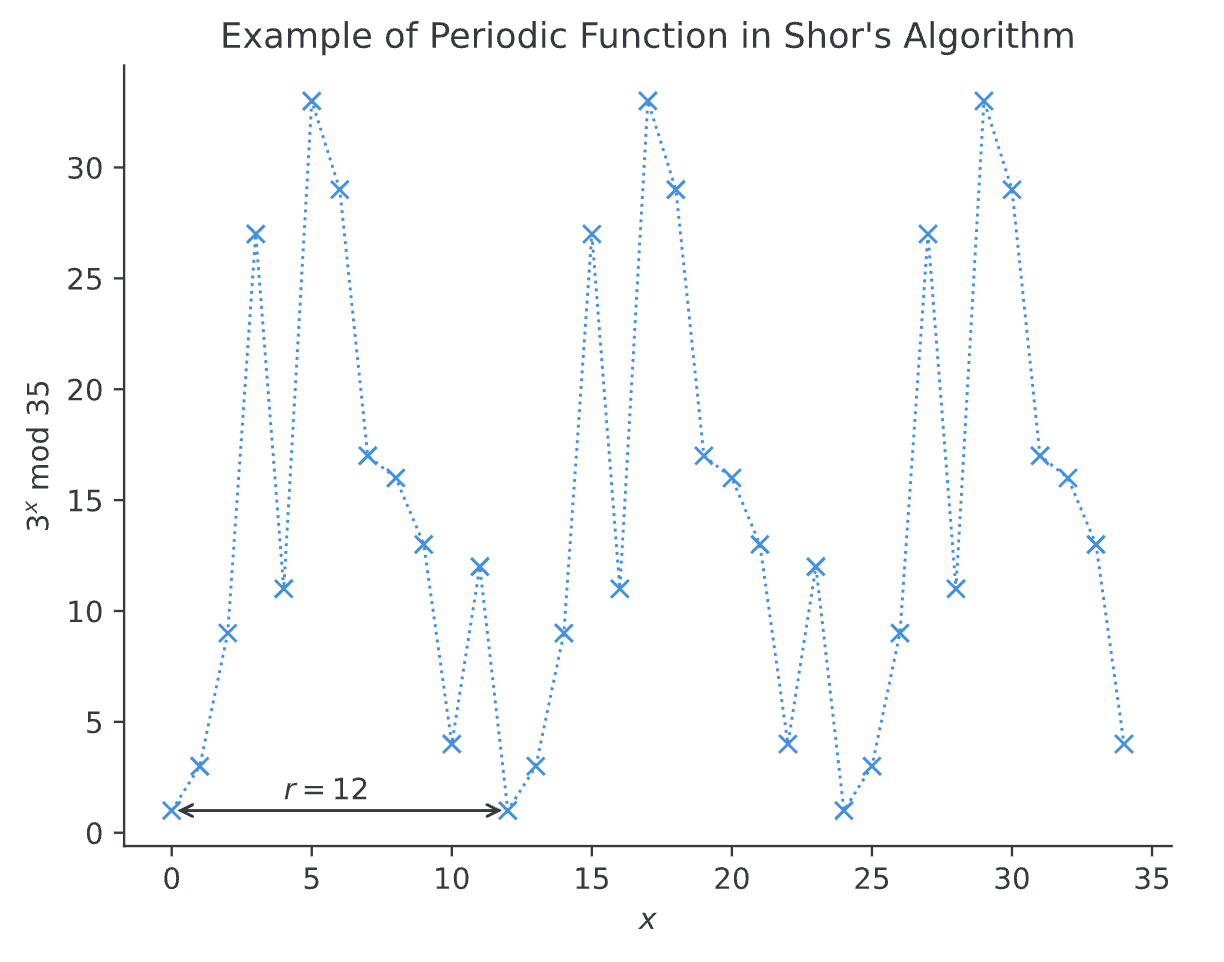
- Once the period is found, compute to discover non-trivial factors of .
Example: Factoring a Small Number with Shor’s Algorithm
Below is a simplified Python-style pseudo-code using Qiskit. This example can factor very small numbers (like 15, 21), illustrating core concepts rather than large-scale factorization. More info here
from qiskit import QuantumCircuit, ClassicalRegister, QuantumRegister, Aer, execute
from qiskit.circuit.library import QFT
def shor_factor(N):
"""
Pseudo-code function to demonstrate the structure
of a Shor's Algorithm circuit for a small integer N.
For large N, a significantly more complex circuit and
quantum resources are required.
"""
# 1. Choose a random 'a' coprime to N
a = find_random_coprime(N) # Placeholder function
# 2. Determine number of qubits needed for the range [0 .. 2^m-1] ~ N^2
m = 4 # For demonstration, a small circuit
# Quantum registers: 'x' for superposition, 'f' to store a^x mod N
x = QuantumRegister(m, name='x')
f = QuantumRegister(m, name='f')
c = ClassicalRegister(m, name='c')
circuit = QuantumCircuit(x, f, c)
# 3. Initialize x register to superposition (Hadamard transforms)
for qubit in x:
circuit.h(qubit)
# 4. Implement the modular exponentiation a^x mod N on the 'f' register
# (Pseudo-code: in reality, this is done via repeated modular multiplications)
circuit = apply_mod_exp(circuit, x, f, a, N)
# 5. Apply Quantum Fourier Transform (QFT) to the x register
qft_dagger = QFT(num_qubits=m, do_swaps=False).inverse()
circuit.append(qft_dagger.to_instruction(), x[:])
# 6. Measure x register
circuit.measure(x, c)
# 7. Run on a simulator
simulator = Aer.get_backend('aer_simulator')
result = execute(circuit, simulator, shots=1024).result()
counts = result.get_counts()
# Use classical post-processing on the measurement result (period-finding)
# Try GCD steps with a^(r/2) ± 1 to find non-trivial factors of N
# ...
return possible_factors
if __name__ == "__main__":
# Example usage:
N = 15 # For demonstration (factors: 3 and 5)
factors = shor_factor(N)
print("Candidate factors:", factors)